
#OBTUSE TRIANGLE TESSELLATION PATCH#
The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling.

Penrose tilings are self-similar: they may be converted to equivalent Penrose tilings with different sizes of tiles, using processes called inflation and deflation. Roger Penrose in the foyer of the Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, standing on a floor with a Penrose tiling
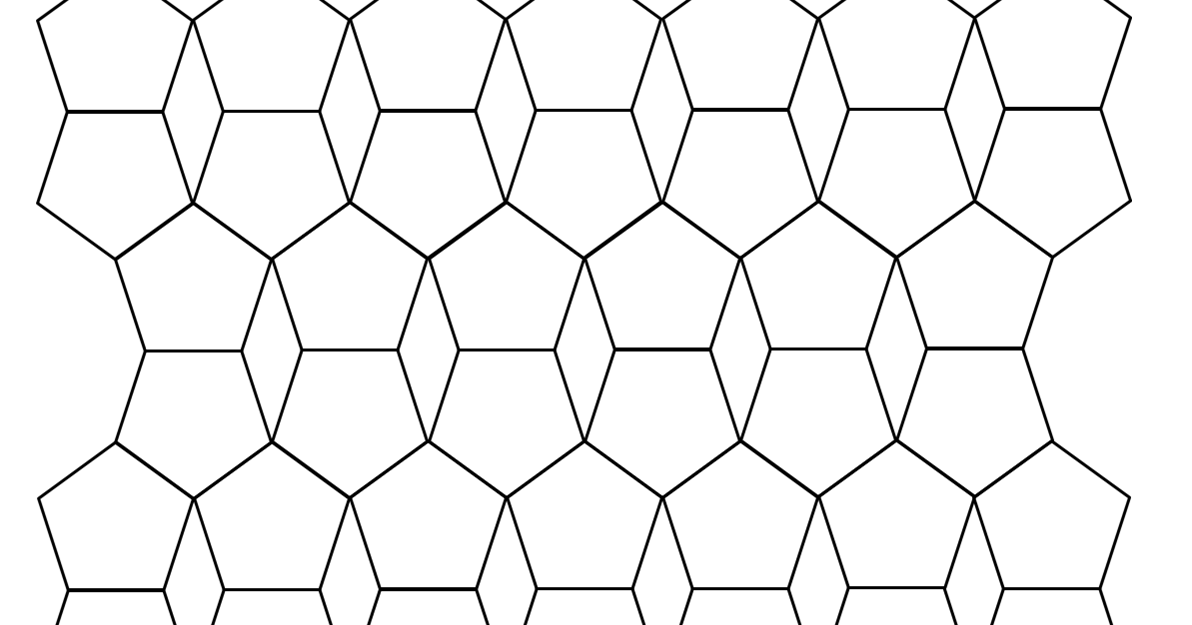
Even constrained in this manner, each variation yields infinitely many different Penrose tilings. This may be done in several different ways, including matching rules, substitution tiling or finite subdivision rules, cut and project schemes, and coverings. The Penrose tilings are obtained by constraining the ways in which these shapes are allowed to fit together in a way that avoids periodic tiling. The original form of Penrose tiling used tiles of four different shapes, but this was later reduced to only two shapes: either two different rhombi, or two different quadrilaterals called kites and darts. There are several different variations of Penrose tilings with different tile shapes. Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated them in the 1970s. However, despite their lack of translational symmetry, Penrose tilings may have both reflection symmetry and fivefold rotational symmetry. Here, a tiling is a covering of the plane by non-overlapping polygons or other shapes, and a tiling is aperiodic if it does not contain arbitrarily large periodic regions or patches. Part of my interest in this surface is that it appears as an abelian differential on Klein's quartic curve, the genus 3 surface with the largest possible group of automorphisms.A Penrose tiling with rhombi exhibiting fivefold symmetryĪ Penrose tiling is an example of an aperiodic tiling. The (1,2,4)-triangle is known not to be a lattice triangle, and in fact its Veech group is unknown perhaps it only includes the order 7 rotation.
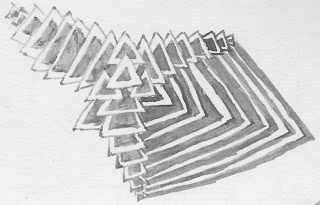
It is also commensurable with with Kepler's small stellated dodecahedron (a description is given by Weber), which is naturally a meromorphic quadratic differential on a genus 4 surface. The (1,1,8)-triangle and the (1,2,2)-triangle unfold to give essentially the same surface: it may be thought of as a pair of stellated pentagons glued along their parallel sides, or as a double cover of the regular decagon surface, branched at the central point. The unfolded (1,4,7)-triangle discovered by Hooper, genus 4 The unfolded (3,5,7)-triangle discovered by Vorobets, genus 4, associated with E8 The unfolded (2,3,4)-triangle discovered by Kenyon and Smillie, genus 3, associated with E7 The unfolded (3,4,5)-triangle discovered by Veech, genus 3, associated with E6 Two "rotations", related by a half-turn if n is odd and by a quarter-turn if n is even. Triangles to see a fundamental domain for the action of the Veech group for each we provide Sufficiently large portion of the tessellation arising from each of these four exceptional Was discovered by Pat Hooper and differs from the others by being obtuse.

To the exceptional Dynkin-Coxeter diagrams E6, E7, and E8 by Chris Leininger, while the fourth Knowledge only four known "exceptional" lattice triangles. There are several known (and related) infinite families of lattice triangles, but to my Original triangle is called a lattice triangle. If the Veech group of this surface is a lattice, then the Any such triangle unfolds to give a translation surface tiled by 2n copies Where p, q, and r are positive integers with no common factor and listed in increasing order Rational triangles are parametrized up to scale by the space of triples of integers (p,q,r), Pictures of tessellations Main Presentations Pictures Notes TeachingĪ rational triangle is a Euclidean triangle whose angles are all rational multiples of pi.


 0 kommentar(er)
0 kommentar(er)
